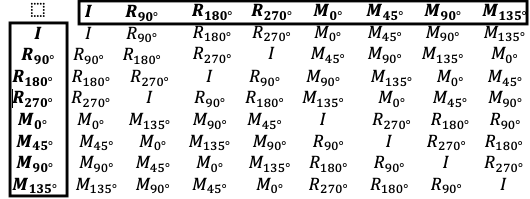I foolishly thought I would be able to write one post every day on this blog, but that ain't happening. I have long debates with myself about the order of the topics, and the order in which I am presenting the topics is nothing like the order of Ted Tracewell's class in the 1970s. No disrespect to Tracewell, I loved him dearly as a teacher and a person. He invited me to dinners at his house, his wife was a great cook, and he introduced me at least once to strangers as "his son". Many math professors at Cal State Hayward called me , and in all modesty, I was a beloved student.
So many topics fold back on themselves in group theory. Its structure is like a complicated watch, and the topics are interconnected in remarkable ways. After learning the basic structure of groups and learning about non-abelian groups where A*B ≠ B*A in all cases, Tracewell taught us about group homomorphisms. Instead, I am going to talk about conjugacy and conjugacy classes first, and I will get to homomorphisms tomorrow, and will likely continue on homomorphisms for the rest of the week.
If you learned the quadratic formula, you should have been taught about complex numbers of the form a∓bi, where i is the imaginary number that solves the equation x² = -1. If the discriminant b²-4ac is negative, the square root in the numerator is imaginary, a multiple of i. The complex numbers a+bi and a-bi are complex conjugates. They are not related to conjugates in group theory, so I wanted to make that clear. Along the same lines, degrees of freedom and degrees in geometry are not related, so I always tried to make that clear when degrees of freedom were introduced in class.
If a = xbx⁻¹, then a and b are conjugates in a group.
If a and b are conjugates in a group, they belong to the same conjugacy class.
Let me go through some of the basics.
1. The identity e is always in a conjugacy class of its own. The reason for this is e commutes with everything so
xex⁻¹ = exx⁻¹ = e.
2. If an element a commutes with all elements in a group G, then a is in a conjugacy class of its own. The reasoning is the same as above.
xax⁻¹ = axx⁻¹ = a.
3. In any abelian group, every conjugacy class contains exactly one element, and such classes are known as singletons.
4. Only in non-abelian groups do we have conjugacy classes with more than one element.
We have only learned so far about one non-abelian finite group, D4, so that will be our example at the end of the post.
5. Conjugacy is a relation that is reflexive, symmetric and transition, and having those three properties means the relation produces equivalency classes, splitting the group G into disjoint sets where the union of all those sets is G itself.
Reflexive. All elements are conjugate to themselves, because eae = a.
Symmetric: if b = xax⁻¹, then x⁻¹bx = x⁻¹xax⁻¹x = a.
Transitive. if b = xax⁻¹ and c = yby⁻¹, then c = yxax⁻¹y⁻¹, and the inverse of yx is x⁻¹y⁻¹.
Now let's look at the conjugacy classes of the symmetries of the square D4. Here, because this table is based on matrices, the identity is called I instead of e.
The I stands alone, so our first conjugacy class is {I}.
If you inspect the row for R180° and the column for R180°, you will see that R180° commutes with everything, so the second conjugacy class is {R180°}.
The two remaining rotations do not commute with the mirrors. We need to do all the possible version of Mx°R90°Mx° to prove my next statement, but I will skip to the result, our third conjugacy class is {R90°,R270°}.
And now we need to find the conjugacy classes for the Mx° elements. Again, the reader should check my work, but you will find there are two more conjugacy classes, {M