The abelian group Z8 is as uncomplicated as a group of order 8 can get. It has a subgroup order 4, another of order 2, and a third of order 1, which is to say the identity. Let's represent it as an additive group and make the Hasse diagram of the subgroup structure.
The structure of subgroups is like nesting Russian dolls, where the next smallest subgroup always fits inside the previous set in the structure.
Easy peasy, lemon squeezy.
We have not yet explored the group structure of the subgroups of order 4 that contain two reflections. Tomorrow, we will look at the Cayley table and Hasse diagram of this abelian group known as the Klein four-group or Z2×Z2.


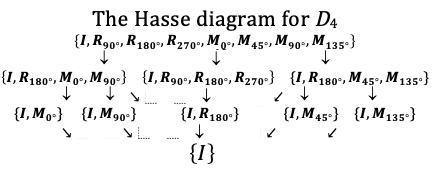

No comments:
Post a Comment